Do you want to make a vector mapping application with quickly responding slippy style panning and scroll wheel zooming, but find it is a lot harder than plotting a simple x, y series? This technique may help. This project presents an application of the Sutherland-Hodgman polygon clipping algorithm for fast conversion of cylindrical coordinates into integer pixel coordinates while seamlessly handling the wrap-around and edge clipping.
Cylindrical map projections such as Mercator, Equidistant, Equal-area, etc. present the Earth as if projected onto a tube. The tube is sliced somewhere along its longitudinal axis and unrolled to create a flat rectangular map. Content on the right hand side of the flat map disappears into the border and comes out along the left hand side. Panning the map with the cursor gives the visual impression of a tube being rolled about its vertical axis.
When rendering a multipoint line vector to the screen, depending on the
viewport and the scale, the line may be entirely on the screen. It may
disappear off the screen and not come back, or it may come back on the same side
or on the opposite side. Most graphics rendering toolkits handle the case of
the line disappearing and returning on the same side fairly well, but none
handle the case of the line wrapping from one side to the other.
Another common difficulty encountered is sending too many points or points that are too far away to the drawing toolkit. Sending too many points can cause severe performance degradation. Organizing your map data into tiled or some other logical form to reduce the amount of data by zoom level can be time consuming. In the case of the Xlib toolkit, the point pixel coordinates are represented by 16 bit short integers. If the scale is adjusted such that it is closely zoomed in, the span of longitude and latitude points can in some cases exceed the maximum short value of 65535.
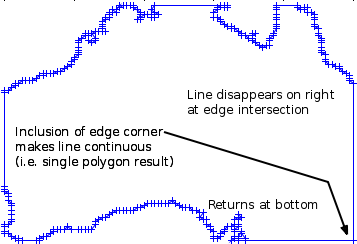
The Sutherland-Hodgman polygon clipping algorithm checks each polygon point in the line in turn against each of the four sides of the rectangle that represents your window. Whenever the current point transitions from inside to outside or outside to inside, the point-slope line intersection formula (y = mx + b) is applied to find a new point exactly on the edge of the screen. By passing only the inside or intersected points from one edge to the next edge, the window corner points get included when the polygon exits on one edge and re-enters on a different edge. By carrying the outside portion of the polygon along the edge of the screen, the algorithm guarantees a result of no more than one polygon.
